Question

What is the equation of the parabola shown below, given a focus at F(−2, 5) and a directrix of y = −1? In addition, identify the vertex and the equation of the axis of symmetry of the parabola.

Answer 1

Answer:

The equation of the parabola is:

`y=(1)/(12)(x+2)^2+2`

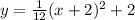
The vertex, (h, k) = (-2, 2)

The equation of the axis of symmetry is x = -2

Option A is the correct choice

Step-by-step explanation:

The focus, (h, f) = (-2, 5)

That is, h = -2, f = 5

The directrix, y = -1

The distance from the focus to thevertex = f - k

The distance from the vertex to the directrix = k - (-1)

The distance from the vertex to the directrix = k + 1

f - k = k + 1

Since f = 5

5 - k = k + 1

k + k = 5 - 1

2k = 4

k = 2

The vertex, (h, k) = (-2, 2)

The equation of the parabola is of the form:

y = a(x - h)² + k

`\begin{gathered} \text{where a = }(1)/(4(f-k)) \\ a=(1)/(4(5-2)) \\ a=(1)/(12) \end{gathered}`

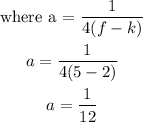
Substititute a = 1/12, h = -2, and k = 2 into the equation y = a(x - h)² + k

`\begin{gathered} y=(1)/(12)(x-(-2))^2+2 \\ y=(1)/(12)(x+2)^2+2 \end{gathered}`

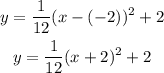
The equation of the parabola is:

`y=(1)/(12)(x+2)^2+2`

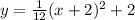
The axis of symmetry of the parabola is the equation of the x-axis of the vertex

x = h

x = -2

The equation of the axis of symmetry is x = -2