Vertex Form of a quadratic equation
A quadratic equation has the vertex form:

Where (h,k) is the vertex of the parabola and a is the leading coefficient.
If a is positive, the parabola is concave up, if a is negative, the parabola is concave down.
We'll identify each graph with a number so we can relate them with their corresponding equation.
Graph 1. Has the vertex at (-5,7) and opens up. The equation of this parabola (for a=1) is:
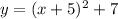
Graph 2 has the vertex at (5,7) and opens up. The equation is:
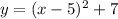
Graph 3 has the vertex at (5,-7) and opens up. The equation is
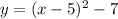
Graph 4 has the vertex at (5,-7) and opens down. The equation is
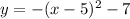
Graph 5 has the vertex at (-5,-7) and opens up. The equation is
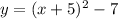
Finally, graph 6 has the same vertex as graph 5 and opens up also, but it grows much faster than that one. The difference is that the leading factor is greater than one. This corresponds to the equation
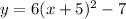
The image below shows the correspondence between the graphs and their equations labeled with numbers.