(1) From the information given, if we want to choose 5 colors from 8 distinct colors and the order in which the selection is made is relevant, then what we have is a permutation.
The formula is given as;
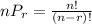
This formula means we need to select/arrange r items out of a total of n items and the anwer derived would be the total number of arrangements possible.
Therefore, we would have;
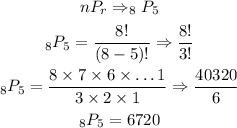
Therefore, if the order is relevant, this selection can be done in 6,720 ways.
(2) If the order is NOT relevant, then what we need to calculate is a combination and the formula is;
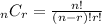
The formula can now be applied as follows;
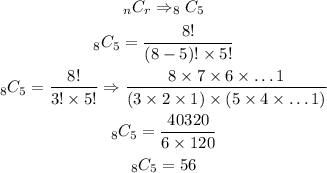
If the order is not relevant, then the selection can be done in 56 ways.