1 Answer

Olubukola · Answer 1 · 2023-11-09T07:41:23+0000

Since we have that BD is the median, it divides the segment or side of the triangle into two equal parts. Then, we have that:

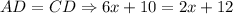
$AD=CD\Rightarrow6x+10=2x+12$

Then, we need to solve the equation for x, and to do so, we need to:

1. Subtract 2x, and 10 from both equations:

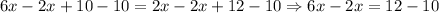
$6x-2x+10-10=2x-2x+12-10\Rightarrow6x-2x=12-10$

2. Since we have like terms, then we have:

$6x-2x=12-10\Rightarrow4x=2\Rightarrow(4)/(4)x=(2)/(4)\Rightarrow x=(2)/(4)\Rightarrow x=(1)/(2)$

In the previous step, we divide both sides of the equation by 4 and then simplify the resulting fraction.

Hence, the value for x = 1/2. The length of AC is the sum of AD + CD or twice the value of one of them:

$AD+CD=6x+10+2x+12=6\cdot(1)/(2)+10+2\cdot(1)/(2)+12=(6)/(2)+10+(2)/(2)+12$

Therefore, the length of AC is

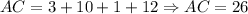
$AC=3+10+1+12\Rightarrow AC=26$

AC = 26 units.

Please log in or register to add a comment.