Since we have that every day the cells die by a third, then that means that after the first day, we only have 2/3 of the cells left. After the second day, we have 2/3 of the day before. Then we would have the following function:
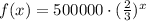
where x is the day and f(x) would be the number of cells left.
Now, we want to know how many days will Alexis have until there are less than 100 cells left. We can write this using this expression:
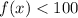
Then, we have:
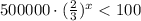
Solving for x we get:
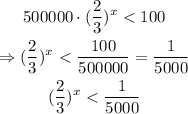
now we apply natural logarithm on both sides of the inequality to get the following:
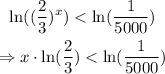
we have that ln(2/3) = -0.4054, then when we move the term to the other side of the inequality, the inequality sign must change:
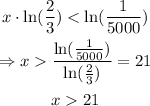
finally, we have that x>21. This means that we need more than 21 days to get less than 100 cells left. We can verify this if we use x=21 on f(x):
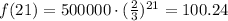
therefore, for x=22, we get:
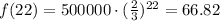
we have that Alexis have 22 days before there are less than 100 cells left