Question:
Simplify the trig expression. sin x tan x +cos x.
Solution:
Let the following trigonometric expression:
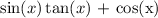
Rewriting using trigonometric identities:
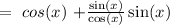
this is equivalent to:
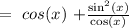
Converting cos (x) to a fraction, this is equivalent to:
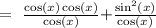
Since the denominators are the same, we can combine the fractions:
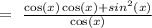
this is equivalent to:
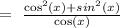
this is equivalent to:
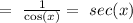
then, we can conclude that the correct answer is :
