Question

Note: Enter your answer and show all the steps that you use to solve this problem in the space provided. Find all cube roots of the complex number 64(cos(219°)+i sin(219°)Leave answers in polar form and show all work.

Answer 1

Step-by-step explanation

We must find the complex cubic roots of the complex number:

`z=64\cdot(\cos(219\degree)+i\sin(219\degree)).`

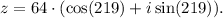
We identify the modulus r and angle θ as:

• modulus r = 64,

,

• angle θ = 219°.

The k = 0, 1, ..., n - 1 roots of a complex number are given by:

`w_k=\sqrt[n]{r}\cdot\lbrack\cos((\theta+k\cdot360\degree)/(n))+i\cdot\sin((\theta+k\cdot360\degree)/(n))]`

In this case three roots, we have k = 0, 1, 2. Using the data and formula from above, we have:

`\begin{gathered} w_0=\sqrt[3]{64}\cdot\lbrack\cos((219\degree+0\cdot360\degree)/(3))+i\cdot\sin((219\degree+0\cdot360\degree)/(3))]=4\cdot\lbrack\cos(73\degree)+i\cdot\sin(73\degree)], \\ w_1=\sqrt[3]{64}\cdot\lbrack\cos((219\degree+1\cdot360\degree)/(3))+i\cdot\sin((219\degree+1\cdot360\degree)/(3))]=4\cdot\lbrack\cos(193\degree)+i\cdot\sin(193\degree)], \\ w_2=\sqrt[3]{64}\cdot\lbrack\cos((219\degree+2\cdot360\degree)/(3))+i\cdot\sin((219\degree+2\cdot360\degree)/(3))]=4\cdot\lbrack\cos(313\degree)+i\cdot\sin(313\degree)]. \end{gathered}`Answer

There are three cubic roots:

`\begin{gathered} w_0=4\cdot\lbrack\cos(73\degree)+i\cdot\sin(73\degree)] \\ w_1=4\cdot\lbrack\cos(193\degree)+i\cdot\sin(193\degree)] \\ w_2=4\cdot\lbrack\cos(313\degree)+i\cdot\sin(313\degree)] \end{gathered}`