Question

¯¯¯¯¯¯ A B has one endpoint located at A ( 4.5, − 3 ) and the midpoint is located at M ( 1,2 ) . What is the location of the other endpoint B ?

Answer 1

Answer:

(-2.5, 7)

Explanations:

The coordinates of the endpoint at A = (4.5, -3)

That is, (x₁, y₁) = (4.5, -3)

The coordinates of the midpoint at M = (1, 2)

That is, (a, b) = (1, 2)

Let the coordinates of the endpoint at B be represennted by (x₂, y₂)

The diagram representing the illustration is shown below:

The coordinates of the midpoint are given by the formulae:

`\begin{gathered} a\text{ = }\frac{x_1+x_2_{}}{2} \\ b\text{ = }\frac{y_1_{}+y_2}{2} \end{gathered}`

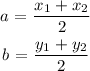
x₁ = 4.5, a = 1, solve for x₂

`\begin{gathered} 1\text{ = }(4.5+x_2)/(2) \\ 2=4.5+x_2 \\ x_2=\text{ 2 - 4.5} \\ x_2=\text{ -2.5} \end{gathered}`

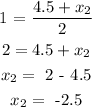
y₁ = -3, b = 2, solve for y₂

`\begin{gathered} 2\text{ = }(-3+y_2)/(2) \\ 4=-3+y_2 \\ y_2=\text{ 4 + 3} \\ y_2=\text{ 7} \end{gathered}`

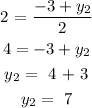
The coordinates, (x₂, y₂) = (-2.5, 7)

The location of the other endpoint B is B(-2.5, 7)