We have the following general rule to find the length of an arc:
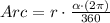
where r is the radius and alpha is the measure of the central angle in degrees.
In this case, we have that r = 8 and alpha equals 270 degrees, since that is the measure of the angle that completes the full circumference, then:
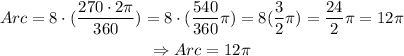
therefore, the length of the gray arc is 12 pi