The word "COLLABORATION" has 13 letters with the following letter count.
C - 1
O - 3
L - 2
A - 2
B - 1
R - 1
T - 1
I - 1
N - 1
The formula for finding permutation with repeated elements is
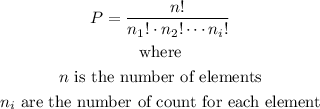
Using the above given, since there are 13 letters, which is a total of 13 elements, and for each element we have
![P=\frac{13!}{1!\cdot3!\operatorname{\cdot}2!\operatorname{\cdot}2!\operatorname{\cdot}1!\operatorname{\cdot}1!\operatorname{\cdot}1!\operatorname{\cdot}1!\operatorname{\cdot}1!}]()
Since 1! = 1, then we can simplify it as
![\begin{gathered} P=\frac{13!}{3!\operatorname{\cdot}2!\operatorname{\cdot}2!} \\ P=\frac{6227020800}{6\operatorname{\cdot}2\operatorname{\cdot}2} \\ P=(6,227,020,800)/(24) \\ P=259459200 \end{gathered}]()
Therefore, the number of permutations of the word "COLLABORATION" is 259,459,200.