Question

How many distinct ways are there to arrange 3 clear marbles, 4 yellow marbles, and 2 orange marbles in a row? Give your answer as an integer.

Answer 1

1260 ways

Step-by-step explanation:

The number of ways in which we can arrange n objects where not all are distinct can be calculated as:

`(n!)/(n_1!n_2!n_3!)`

Where n is the total number of marbles, and n1, n2, and n3 are the number of marbles of each color. So, there are 9 marbles in total, 3 clear, 4 yellow, and 2 orange.

Then, replacing n by 9, n1 by 3, n2 by 4, and n3 by 2, we get:

`\frac{9!}{3!\cdot4!\cdot2!^{}}=1260`

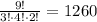
Therefore, there are 1260 distinct ways to arrange the marbles.