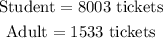Let 'x' represent the number of students tickets.
Let 'y' represent the number of adults tickets.
Two equations will be formed from the statements.
We were told that the total number of tickets sold is 9536 tickets.
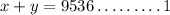
The total cost of the tickets is $56,878.
Given that tickets are selling for students $5(under 18) and for Adults $11(18+).

Let us now combine the two equations and solve for x and y using the substitution method.
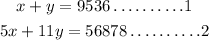
Solving for x and y
Isolate x for x + y = 9536
x = 9536 - y
Substitute x = 9536 - y into equation 2
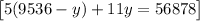
Simplify
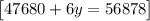
Solve for y

For x = 9536 - y
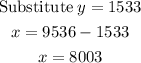
The solution to the system of equations is,
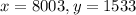
Hence, the number of tickets sold are