Question

What is multiplied to get -50 but adds to 5

Answer 1

The Solution:

The question says two numbers are multiplied to get -50, but when added we get 5.

To find the two numbers, we shall say

Let one of the numbers be a, and the other b.

So that

`\begin{gathered} ab=-50\ldots eqn(1) \\ a+b=5\ldots eqn(2) \end{gathered}`

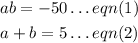
Solving both equations simultaneously by the substitution method, we get

`\begin{gathered} \text{From eqn(2), we find a:} \\ a=5-b\ldots eqn(3) \end{gathered}`

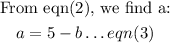
Putting eqn(3) into eqn(1), we get

`\begin{gathered} (5-b)b=-50 \\ \text{Clearing the bracket, we get} \\ 5b-b^2=-50 \\ b^2-5b-50=0 \end{gathered}`

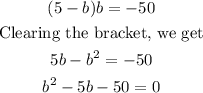
Solving the above quadratic equation by the Factorisation Method, we get

`\begin{gathered} b^2-10b+5b-50=0 \\ b(b-10)+5(b-10)=0 \\ (b+5)(b-10)=0 \end{gathered}`

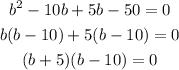
So,

`\begin{gathered} b+5=0\text{ or b-10=0} \\ b=-5\text{ or b=}10 \end{gathered}`

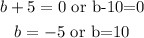
Substituting -5 or 10 for b in eqn(3), we get

`\begin{gathered} a=5--5=5+5=10 \\ or \\ a=5-10=-5 \\ So, \\ a=10,b=-5 \\ or \\ a=-5,b=10 \end{gathered}`

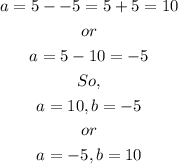
So, the two numbers are -5 and 10.

Therefore, the correct answers are -5 and 10