Question

For the given cosine function:A. Identify the amplitudeB. Use the period to calculate bC. Identify the phase shiftD. Identify the midline valueE. Write the equation

Answer 1

ANSWER and EXPLANATION

(A) The amplitude of the function is half the difference between the maximum and minimum value of the function.

Hence, the amplitude is:

`\begin{gathered} A=(210-10)/(2) \\ A=(200)/(2) \\ A=100\text{ ft} \end{gathered}`

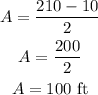
(B) The period is the time taken for one complete cycle. From the graph, the period is 90 seconds.

Hence, the value of b is:

`\begin{gathered} b=(2\pi)/(period) \\ b=(2\pi)/(90) \\ b=(\pi)/(45) \end{gathered}`

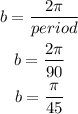
(C) The phase shift of the graph is the distance between the vertical axis and the start point of the graph. The graph is a cosine graph, hence, the start point is its peak.

Hence, the phase shift is:

`c=30`

(D) The midline value of the graph is given to be:

`110`

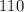
(E) The general form for the equation of a cosine function is:

`y=A\cos(bx+c)+d`

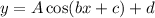
where A = amplitude

b = periodicity

c = horizontal shift

d = vertical shift/midline

Hence, the equation of the cosine function is:

`y=100\cos((\pi)/(45)x+30)+110`