Since HG is the perpendicular bisector of MN, NH=HM; thus, HM=8. Furthermore,
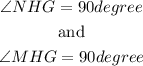
Thus, NHG and MHG are right triangles that have two sides of equal length
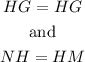
Therefore,
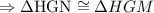
Finally,
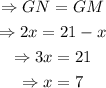
And the perimeter of triangle MNG is
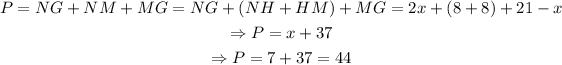
Therefore, the answers are x=7, and the Perimeter of MNG is equal to 44