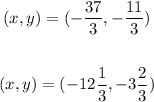Question

please help I have been trying to get this for a long timeSolve x = 8y + 17 → (1) x = 5y + 6 →(2)

Answer 1

Given the system of equations:

x = 8y + 17 → (1)

x = 5y + 6 →(2)

by substitution by x from the first equation in the second equation

`8y+17=5y+6`

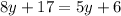
Solve the equation for y

Combine the like terms

`\begin{gathered} 8y-5y=6-17 \\ 3y=-11 \\ \\ y=-(11)/(3) \end{gathered}`

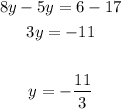
Substitute with y in the first equation to find x

`\begin{gathered} x=8\cdot-(11)/(3)+17 \\ \\ x=-(88)/(3)+17=-12(1)/(3)=-(37)/(3) \end{gathered}`

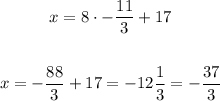
So, the solution of the system as order pair :

`\begin{gathered} (x,y)=(-(37)/(3),-(11)/(3)) \\ \\ (x,y)=(-12(1)/(3),-3(2)/(3)) \end{gathered}`