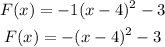Question

The graph of F(X), shown below, resembles the graph of G(X) = x2, but it hasbeen stretched somewhat and shifted. Which of the following could be theequation of F(x)?5GO) = x25nFO) = ?A. F(X) = (x - 4)2-3B. F(x) = (x + 4)2-3C. F(x) = -(x + 4)2-3D. F(x) = -(x-4)2-3

Answer 1

Answer:
`F(x)=-(x-4)^2-3`

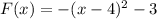
Explanations:

Both functions F(x) and G(x) represent a parabola

G(x) = x²

A parabolic function is always of the form:

`F(x)\text{ = }a(x-h)^2+k`

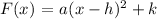
The point (h, k) is the vertex of the graph F(x)

From the graph shown, h = 4, k = -3

Since the graph does not intersect the x and y axes and it is facing downwards, the amplitude a = -1

Substituting a = -1, h = 4, and k = -3 into the given equation

`\begin{gathered} F(x)=-1(x-4)^2-3 \\ F(x)=-(x-4)^2-3 \end{gathered}`