Question

At the movie theatre, child admission is $5.10 and adult admission is $9.80. On Friday, three times as many adult tickets as child tickets were sold, for a total sales of $1311.00. How many child tickets were sold that day? Number of child tickets:

Answer 1

The given information is:

- Cost of each child ticket: $5.10

- Cost of each adult ticket: $9.80

- They sold 3 times as many adult tickets as child tickets

- The total sales were $1311.00

So, we can express this situation in the form of algebraic equations:

Let's set "A" as the number of adult tickets sold, and "C" as the number of child tickets sold, so:

`A=3C\text{ Equation 1}`

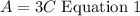
Now, the total sales are given by:

`5.10*C+9.80*A=1311.00\text{ Equation 2}`

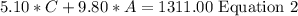
Replace equation 1 into equation 2 and solve for C:

`\begin{gathered} 5.10C+9.80(3C)=1311.00 \\ 5.10C+29.40C=1311.00 \\ 34.50C=1311.00 \\ C=(1311.00)/(3.50) \\ C=38 \end{gathered}`

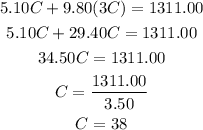
Now, replace C-value into equation 1 and solve for A:

`\begin{gathered} A=3*38 \\ A=114 \end{gathered}`

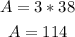
Then, there were sold 38 child tickets and 114 adult tickets.