The equation of a line can be represented in many forms. We are to express the equation in slope intercept form.
The general formula used for the slop-intercept formulation is as follows:
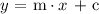
Where,

The equation of a line allow us to determine the coordinates of any point on the line by stating its coordinates in the form, in the cartesian coordinate system:
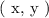
From the general slop-intercept formulation expressed initially we see that we have two constants ( m & c ). These constants are determined using points that lie on the line. These very same constants also makes an equation of a line unique from all the other equations.
From the data given, The slope of the line is 2. We will go ahead and assign the value to the constant m as follows:
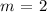
Then we plug in the value of intercept in the initial general slop-intercept form as follows:
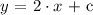
Now to evaluate the constant ( c ) we need a pair of coordinates that must lie on the line for which the equation is derived. The data provides us with this point as:
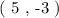
We will go ahead and plug in the respective coordinates in the slope-intercept form derived above:
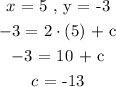
We have determined the two constants ( m & c ). Now to express the unique equal