Question

Find the area of an equilateral triangle with side lengths of 10ft. (round to the nearest tenth)

Answer 1

The area of the triangle is;

`43.3\text{ square ft}`

Step-by-step explanation:

Given an equilateral triangle with sides 10ft.

Recall that the area of a triangle can be calculated using the formula;

`A=(1)/(2)bh`

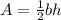
The height of the triangle would be;

`\begin{gathered} h=\sqrt[]{10^2-5^2} \\ h=\sqrt[]{75}^{} \\ h=5\sqrt[]{3} \end{gathered}`

and the base length is;

`b=10`

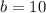
substituting;

`\begin{gathered} A=(1)/(2)bh=(1)/(2)*10*5\sqrt[]{3} \\ A=25\sqrt[]{3} \\ A=43.3\text{ square ft} \end{gathered}`

Therefore, the area of the triangle is;

`43.3\text{ square ft}`