Given the expression:
![9\cdot\sqrt[]{125}](https://img.qammunity.org/2023/formulas/mathematics/college/y267osmvc4c6319l42adow8b21ioyplgob.png)
notice that for 125 we have the following:
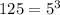
therefore, we can simplify the expression by using 5^3 to get the following:
![9\cdot\sqrt[]{125}=9\cdot\sqrt[]{5^3}=9\cdot\sqrt[]{5^2\cdot5}](https://img.qammunity.org/2023/formulas/mathematics/college/mpxx0pt8pa79axg637o12kgy8blp906qqb.png)
now, remember that when we have a product inside a square root, we can split it on both factors. In general, for any exponent, we have the following rule:
![\begin{gathered} (a\cdot b)^n=a^nb^n \\ \text{ in this case:} \\ \sqrt[]{a\cdot b}=\sqrt[]{a}\cdot\sqrt[]{b} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/br0z81i89qsewx43h8t65zsb1n5yls9yhx.png)
then, for our expression at hand, we have:
![9\cdot\sqrt[]{5^2\cdot5}=9\cdot\sqrt[]{5^2}\cdot\sqrt[]{5}=9\cdot5\cdot\sqrt[]{5}=45\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/m05jsl6q16vd390t2mubiuxwfz6f11gpax.png)
therefore, the simplifed expression is 45*sqrt(5)