Question

xP(x)00.0510.1520.130.7Find the standard deviation of this probability distribution. Give your answer to at least 2 decimal places

Answer 1

We have to find the standard deviation of this probability distribution.

We have to start by calculating the mean of this distribution.

It can be calculated as:

`\begin{gathered} \bar{x}=\sum^nP(x_i)\cdot x_i \\ \bar{x}=0.05\cdot0+0.15\cdot1+0.1\cdot2+0.7\cdot3 \\ \bar{x}=0+0.15+0.2+2.1 \\ \end{gathered}`

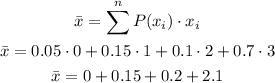
We now can calculate the standard deviation using the last result as:

`\begin{gathered} \sigma=\sqrt{\sum_^P(x_i)\cdot(x_i-\bar{x})^2} \\ \sigma=√(0.05(0-2.1)^2+0.15(1-2.1)^2+0.1(2-2.1)^2+0.7(3-2.1)^2) \\ \sigma=√(0.05(-2.1)^2+0.15(-1.1)^2+0.1(-0.1)^2+0.7(0.9)^2) \\ \sigma=√(0.05(4.41)+0.15(1.21)+0.1(0.01)+0.7(0.81)) \\ \sigma=√(0.2205+0.1815+0.001+0.567) \\ \sigma=√(0.97) \\ \sigma\approx0.98 \end{gathered}`

Answer: the standard deviation is approximately 0.98.