Given:
(a) A series circuit with 2 light bulbs
(b) A series circuit with 3 light bulbs
(c) A simple circuit with one light bulb
(d) A parallel circuit with two light bulb
Also, light bulbs are identical.
To find the circuit having the greatest amount of current leaving the battery.
Step-by-step explanation:
The light bulb acts as a resistance in the circuit.
As light bulb are identical, let each bulb has R resistance.
The battery supplied is the same, so the voltage is the same.
According to Ohm's law,
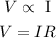
As the voltage is constant, so the current will be
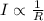
We have to calculate the resistance of each circuit, in order to find the greatest current in the circuit.
The series resistance can be calculated by the formula
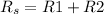
The parallel resistance can be calculated by the formula

(a) The resistance of the series circuit with 2 light bulbs will be
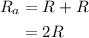
(b) The resistance of the series circuit with 3 light bulbs will be
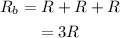
(c) The simple circuit has resistance
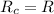
(d) The resistance of the circuit with two resistances will be
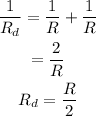
As the resistance of the parallel circuit with two light bulbs is minimum, so the current will be maximum.
Thus, the circuit (d) parallel circuit with two light bulbs has a maximum current leaving the battery.