Question

Given the function f(x)=3/4x^2-x, then what is f(x-1) as a simplified polynomial?

Answer 1

f(x-1) = (3/4)x² - (5/2)x + 7/4

Step-by-step explanation:

To find f(x-1), we need to replace x by (x-1) on the equation of f(x), so

`\begin{gathered} f(x)=(3)/(4)x^2-x \\ f(x-1)=(3)/(4)(x-1)^2-(x-1) \end{gathered}`

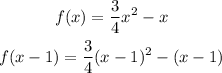
Then, we can simplify the polynomial

`\begin{gathered} f(x_{}-1)=(3)/(4)(x^2-2x+1)-x+1 \\ f(x-1)=(3)/(4)x^2-(3)/(4)(2x)+(3)/(4)-x+1 \\ f(x-1)=(3)/(4)x^2-(3)/(2)x-x+(3)/(4)+1 \\ f(x-1)=(3)/(4)x^2-(5)/(2)x+(7)/(4) \end{gathered}`

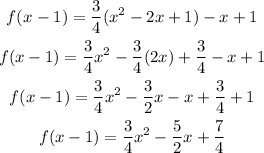
Therefore, the simplified polynomial for f(x-1) is

f(x-1) = (3/4)x² - (5/2)x + 7/4