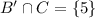Given: Sets B and C are subsets of the universal set U.
These sets are defined as follows-
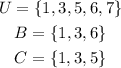
Required: To determine the following sets-
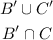
Explanation: The complement of a set A with the universal set U is defined as-
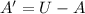
Hence, the complement of set B is-
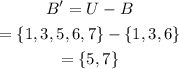
Similarly, the complement of set C is-

Now,
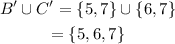
Similarly-
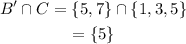
Final Answer: (a)-
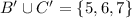
(b)-