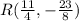A line segment has the following endpoints
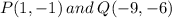
We are asked to find the coordinates of point R, such that the point R will be 3/5 of the distance PQ.
Let us first find the distance from P to Q.
The distance between two points P and Q is given by
![PQ=\sqrt[]{\mleft({x_2-x_1}\mright)^2+\mleft({y_2-y_1}\mright)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/r5euuk39agj4whi0412c7dheefmu6g82us.png)
Let us substitute the given points into the above distance formula
![\begin{gathered} PQ=\sqrt[]{({-9_{}-1_{}})^2+({-6_{}-(-1)_{}})^2} \\ PQ=\sqrt[]{({-9_{}-1_{}})^2+({-6_{}+1_{}})^2} \\ PQ=\sqrt[]{({-10})^2+({-5})^2} \\ PQ=\sqrt[]{100^{}+25^{}} \\ PQ=\sqrt[]{125} \\ PQ=11.18 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/86avcr7k5pg5f6m24hsf41r1n6zssu2uce.png)
Now let us find the coordinates of point R such that R is equal to 3/5 of PQ.
So the ratio is m:n = 3:5
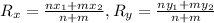
Let us substitute the given values into the above formula
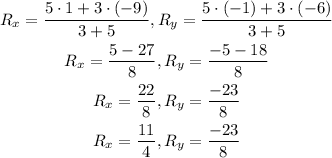
Therefore, the coordinates of the point R is