Given:
The distance to the fishing spot, S=5 miles.
The time taken to reach the fishing spot travelling against the current, t=5/12 h.
The time taken to reach the fishing spot travelling with the current , T=1/4 h.
Now, the speed of the boat when it is travelling in the direction of the current or the downstream speed is,

The speed of the boat when it is travelling in the against the direction of the current or the upstream speed is,
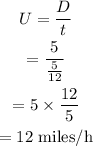
Let b be the speed of the boat in still water and w be the speed of the current.
Hence, the speed of the boat in still water can be calculated as,

The speed of the current can be calculated as,
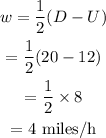
Therefore, the speed of the boat in still water is 16 mph .
The speed of the current is 4 miles mph.