In this problem, a student is doing a test:
• with five multiple-choice questions → n = 5,
,
• containing five options each → probability of guess p = 1/5 = 0.2,
,
• a pass mark of the test of 60%.
We want to know the probability that the student fails the test, i.e. we must compute the probability:

Where X is the number of correct answers and X = 3 = 0.6 * 5 represents a 60% of correct answers in the test.
Now, this probability consists of a binomial probability, which refers to the probability of exactly X successes on n repeated trials in an experiment that has two possible outcomes.
The formula for the binomial probability is:
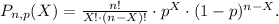
Now, the probability above is given by:
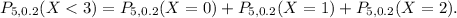
Using the formula above, we compute each term, we get:
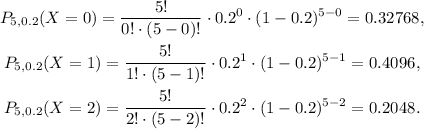
Replacing these values in the formula above, we get:
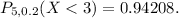
Answer
The probability that the student fails the test is 0.94208.