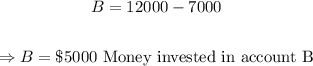Question

Mary invested $12,000 in two different accounts. Account A earns 12% simple interest and Account B earns 8% simple interest. If the total interest at the end of 1 year was $1240, how much was invested in each account.

Answer 1

Let us say that A and B represent the money invested in accounts A and B, respectively.

Then, if Mary invested $12 000 in total:

`A+B=12000...(1)`

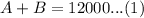
The formula for the simple interest is given by the equation:

`I=r\cdot P\cdot t`

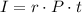
Where r is the annual rate of interest and t is the time (in years).

From the problem, we identify:

`\begin{gathered} r_A=0.12 \\ r_B=0.08 \\ t=1 \end{gathered}`

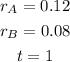
Then, the interests at the end of 1 year for each account are:

`\begin{gathered} I_A=0.12A \\ I_B=0.08B \end{gathered}`

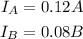
If the total interest is $1240:

`\begin{gathered} I_A+I_B=1240 \\ \\ \Rightarrow0.12A+0.08B=1240...(2) \end{gathered}`

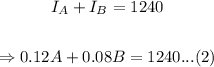
From (1):

`B=12000-A...(3)`

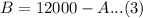
Using (3) in (2):

`\begin{gathered} 0.12A+0.08\left(12000-A\right)=1240 \\ \\ 0.12A+960-0.08A=1240 \\ \\ 0.04A=280 \\ \\ \Rightarrow A=\$7000\text{ \lparen Money invested in account A\rparen} \end{gathered}`

Finally, using this result on (3):

`\begin{gathered} B=12000-7000 \\ \\ \Rightarrow B=\$5000\text{ \lparen Money invested in account B\rparen} \end{gathered}`