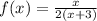Question

give an example of a rational function that has a horizontal asymptote of y=1/2 and vertical asymptote at x=-3

Answer 1

The horizontal asymptote of a function is the value of y when x -> ∞

`\lim _(x\to\infty)f(x)=y`

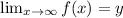
and the vertical asymptote of a function is the x-value when y -> ∞.

For a rational function, the y approaches infinity when the denominator vanishes. In other words, when in q/p, p --> 0.

Using this fact we see that the denominator of our function must vanish at x = -3. This happens when the denominator has the form

`(1)/(x+3)`

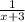
because

`\lim _(x\to-3)(1)/(x+3)=\infty`

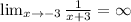
is the vertical asymptote.

For the horizontal asymptote, the function can be of the form

`f(x)=(x)/(2(x+3))`

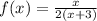
because

`\textcolor{#FF7968}{\lim _(x\to\infty)(x)/(2(x+3))=(1)/(2)}`

Hence the function is

`f(x)=(x)/(2(x+3))`