Solution
Santos takes the train into the city five days a week for work.
For one work week, he kept track of how many minutes long each train ride was:
48, 51, 48, 48, 50
To find the mean of ungrouped data, the formula is
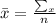
n is the number of data given.
Where n = 5
Substitute the data into the formula above

Hence, the mean is 49
To find the median, we arrange the given data in ascending number and pick the middle number as shown below
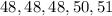
Hence, the median is 48
To find the range, the formula
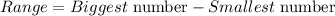
The smallest number is 48
The largest number is 51
Substitute into the formula above
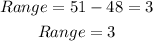
Hence, the range is 3
To find the midrange, the formula is

Substitute the values into the formula above
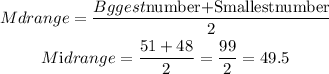
Hence, the midrange is 49.5
Thus, the answer is Mean, 49: Median, 48: Range, 3; Midrange, 49.5