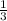Question

Find the probability.A fair die is rolled. What is the probability of rolling a 3 or a 4?A) 1/6B) 1/36C) 1/3D) 2

Answer 1

Given:

A fair die is rolled.

To find:

The probability of rolling a 3 or a 4.

Step-by-step explanation:

The total sample space is,

`\begin{gathered} S=\lbrace1,2,3,4,5,6\rbrace \\ n(S)=6 \end{gathered}`

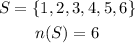
The number of favourable outcomes is,

`\begin{gathered} n(A)=n(Rolling\text{ a 3})=1 \\ n(B)=n(Rolling\text{ a 4\rparen}=1 \end{gathered}`

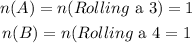
The probability of rolling a 3 or a 4 is,

`\begin{gathered} P(A\cup B)=(n(A))/(n(S))+(n(B))/(n(S)) \\ =(1)/(6)+(1)/(6) \\ =(2)/(6) \\ =(1)/(3) \end{gathered}`

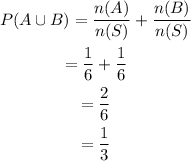
Final answer: Option C

The probability of rolling a 3 or a 4 is,

`(1)/(3)`