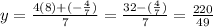We have the following equation given:
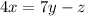
We need to solve for y when x=8 and 7z=-4. If we solve for y we got:
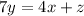
And dividing both sides by 7 we got:
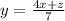
We can use the condition 7z=-4 in order to solve for z and we got:
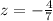
Now we can replace x and z in order to solve for y and we got: