Answer:
Vertex: (-4,3)
roots: (-5,0), (-3,0)
Equation: y = -3 ( x + 5) ( x+3)
Explanation:
As can be seen from the graph given, the vertex of the graph is at (4, 3).
The roots of the function at (-5, 0) and (-3, 0).
The equation of the function can be constructed using the roots of the function.
We know that the equation of a parabola can be written as
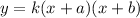
where roots of the function are at (-a, 0 ) and (-b, 0). From this, we deduce that for our function the equation must be
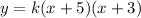
where k is a constant hitherto unknown.
We find the value of k using the point (-4, 3) from which we know that when x = -4, y= 3.
Putting in x = -4 and y = 3 in the above equation gives
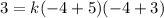
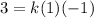
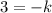
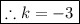
Hence, our equation is
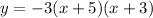
which is our answer!