Question

A circular loop with a radius of 9.792 cm is positioned in various orientations in a uniform magnetic field of 1.194 T. Find the magnetic flux if the normal to the plane of the loop is parallel to the field.

Answer 1

The magnetic flux Φ of a field B on a loop with area A and normal vector n is:

`\Phi=BA\cos\theta`

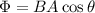
There θ is the angle between the normal vector n and the field B.

If the normal to the plane of the loop is parallel to the field, then θ=0º. In that case, the magnetic flux is simply the product of the field and the area of the loop, since cos(θ)=0:

`\begin{gathered} \theta=0 \\ \Rightarrow \\ \Phi=BA \end{gathered}`

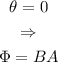
The area of a circle with radius r is:

`A=\pi r^2`

Replace the expression for the area in terms of r and substitute B=1.194T and r=9.792*10^(-2)m to find the magnetic flux:

`\begin{gathered} \Phi=BA \\ \\ =B\cdot\pi r^2 \\ \\ =1.194T\cdot\pi(9.792*10^(-2)m)^2 \\ \\ =0.0359664...Tm^2 \\ \\ \approx0.03597Wb \end{gathered}`

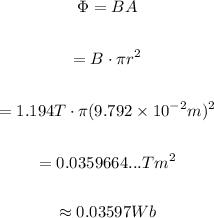
Therefore, the magnetic flux if the normal is parallel to the field, is 0.03597 weber.