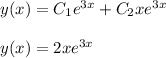Question

Section 5.2 Problem 19:

Solve the initial value problem and graph the solution.

`y'' - 6y' + 9y = 0`

`y(0) = 0`

`y'(0) = 2`
​

Answer 1

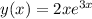`y(x)=2xe^(3x)` (See attached graph)

Explanation:

To solve a second-order homogeneous differential equation, we need to substitute each term with the auxiliary equation
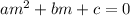`am^2+bm+c=0` where the values of
`m` are the roots:

`y''-6y'+9y=0\\\\m^2-6m+9=0\\\\(m-3)^2=0\\\\m-3=0\\\\m=3`

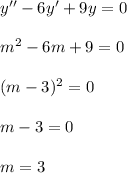
Since the values of
`m` are equal real roots, then the general solution is
`y(x)=C_1e^(m_1x)+C_2xe^(m_1x)`.

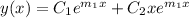Thus, the general solution for our given differential equation is
`y(x)=C_1e^(3x)+C_2xe^(3x)`.

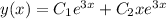To account for both initial conditions, take the derivative of
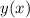`y(x)`, thus,
`y'(x)=3C_1e^(3x)+C_2e^(3x)+3C_2xe^(3x)`

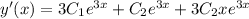
Now, we can create our system of equations given our initial conditions:

`y(x)=C_1e^(3x)+C_2xe^(3x)\\ \\y(0)=C_1e^(3(0))+(C_2)/(6)(0)e^(3(0))=0\\ \\C_1=0`

`y'(x)=3C_1e^(3x)+C_2e^(3x)+3C_2xe^(3x)\\\\y'(0)=3C_1e^(3(0))+C_2e^(3(0))+3C_2(0)e^(3(0))=2\\\\3C_1+C_2=2`

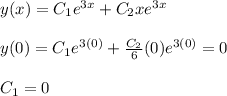
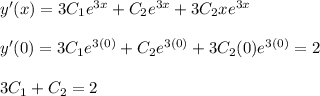
We then solve the system of equations, which becomes easy since we already know that
`C_1=0`:

`3C_1+C_2=2\\\\3(0)+C_2=2\\\\C_2=2`

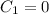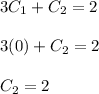
Thus, our final solution is:

`y(x)=C_1e^(3x)+C_2xe^(3x)\\\\y(x)=2xe^(3x)`