Question

A projector displays a rectangular image on a wall. The height of the wall is x feet. The area in square feet of the projection is represented by x^2-12x+32. The width of the projection is (x-4) feet. a. Write a binomial that represents the height of the projection b. Find the perimeter of the projection when the height of the wall is 10 ft.

Answer 1

Given:

The area of the projection is

`A=(x^2-12x+32)ft^2`

The width of the projection is w =(x-4) feet.

Let l be the height of the projection.

The shape of the projection is a rectangle.

Consider the formula for the area of the rectangle.

`A=lw`

`\text{ Sustitute }A=\mleft(x^2-12x+32\mright)\text{ and w=(x-4) in the formula.}`
`x^2-12x+32=l(x-4)`
`Use\text{ }-12x=-8x-4x.`

`x^2-8x-4x+32=l(x-4)`

`x(x-8)-4(x-8)=l(x-4)`

`(x-8)(x-4)=l(x-4)`

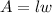
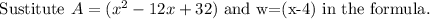
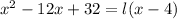
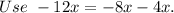
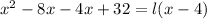
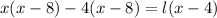
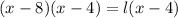
Cancel out the common factor.

`(x-8)=l`

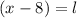
Hence the height of the projection is (x-8).

b)

Given:

Height of the wall x=10 ft.

We know that the width of the projection w =(x-4) and height of the projection l=(x-8).

Substitute x=10 in the equation l and w, we get

`w=10-4=6\text{ ft}`
`l=10-8=2ft`

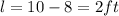
Consider the perimeter of the rectangle.

`P=2(l+w)`

Substitute l=2 and w=10 in the formula, we get

`P=2(2+4)=2*8=16\text{ ft.}`

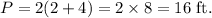
Hence the perimeter of the projection is 16 ft when the height of the wall is 10 ft.