Question

140. (Continuation) The slope of a line is a measure of how steep the line is. It is calculated by dividing the change in y-coordinates by the corresponding change in x-coordinates betweentwo points on the line: slope = change in y . Calculate the slope of the line that goes change in xthrough the two points (1,3) and (7,6). Calculate the slope of the line that goes through the two points (0, 0) and (9, 6). Which line is steeper?

Answer 1

The slope of a line is given by the following equation:

`m=\text{ }(Y2-Y1)/(X2-X1)`

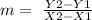
where (X1, Y1) and (X2, Y2) are points on the line. Taking this into account, we have to:

1. Slope of the line that goes through the two points (1,3) and (7,6):

Note that in this case

(X1,Y1) = (1,3)

(X2, Y2)= (7,6)

replacing this data into the slope-equation, we get:

`m=\text{ }(Y2-Y1)/(X2-X1)\text{ = }(6-3)/(7-1)\text{ = }(3)/(6)\text{ = }(1)/(2)\text{ = 0.5}`

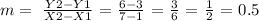
then, the slope of the line that goes through the two points (1,3) and (7,6) is:

`m_1=\text{ }(1)/(2)\text{ = 0.5}`

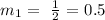
2. Slope of the line that goes through the two points (0,0) and (9,6):

Note that in this case

(X1,Y1) = (0,0)

(X2, Y2)= (9,6)

replacing this data into the slope-equation, we get:

`m=\text{ }(Y2-Y1)/(X2-X1)\text{ = }(6-0)/(9-0)\text{ = }(6)/(9)\text{ = }(2)/(3)\text{ =0.66}\approx0.7`

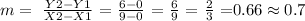
then, the slope of the line that goes through the two points (0,0) and (9,6) is:

`m_2=\text{ 0.66}\approx0.7`

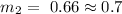
note that

`m_2>m_1`

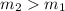
then, we can conclude that the second line ( the line that goes through the two points (0,0) and (9,6) ) is steeper than that the first line (the line that goes through the two points (1,3) and (7,6) ).