Question

Can you help me with this question I can add the answers after

Answer 1

-2.852i + 2.377 j

Step-by-step explanation

We have to find the projection of u onto v,

`proj_vu=\left(\frac{\vec{u}\cdot\vec{v}}v\right)\vec{v}`

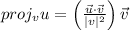
The vectors are:

• u = <-9, -5>

,

• v = <-6, 5>

Let's find the dot product,

`\vec{u}\cdot\vec{v}=u_xv_x+u_yv_y=(-9)(-6)+(-5)(5)=54-25=29`

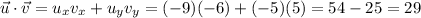
Now, find the modulus of v squared,

`|\vec{v}|^2=v_x^2+v_y^2=(-6)^2+(5)^2=36+25=61`

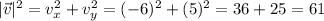
Now, we have to divide 29 by 61 and multiply each of the components of vector v by this constant,

`proj_vu=(29)/(61)\lt-6,5>\text{ }\approx\text{ }\lt-2.852,2.377>`

Hence, the projection is the vector <-2.852, 2.377> or, using another notation, -2.852i + 2.377 j.