Question

What is the inverse of the function f (x) = 3(x + 5)2 – 4, such that x ≤ –5?

Answer 1

`A)f^(-1)(x)=-5+\sqrt[]{(x+4)/(3)}`

1) To find out the inverse function, of that one-to-one function we need to proceed with the following steps:

`f(x)=3(x+5)^2-4,f^(-1)(x)=?`

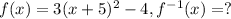
2) Swap the variables, and isolate the y variable on the left side:

`\begin{gathered} f(x)=3(x+5)^2-4 \\ y=3(x+5)^2-4 \\ x=3(y+5)^2-4 \\ -3(y+5)^2=-x-4 \\ (3\mleft(y+5\mright)^2)/(3)=(x+4)/(3) \\ (y+5)^2=(x+4)/(3) \end{gathered}`

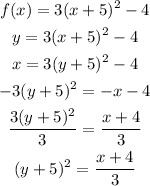
Now we need to get rid of that square binomial, taking the square root on both sides:

`\begin{gathered} (y+5)^2=(x+4)/(3) \\ \sqrt[]{(y+5)^2}=\sqrt[]{(x+4)/(3)} \\ y+5=\sqrt[]{(x+4)/(3)} \\ y=\sqrt[]{(x+4)/(3)}-5 \\ f^(-1)(x)=\sqrt[]{(x+4)/(3)}-5 \end{gathered}`

And that is the final answer.