Question

Alice’s company has a machine that can be produce a maximum of 2722 components annually. She sells each component for $65. The company’s fixed costs are $35,120 per annum and the variable costs are $25 per component.

Answer 1

Explanation

We are given the following information:

• Alice's company has a machine that can be produce a maximum of 2722 components annually.

,

• She sells each component for $65.

,

• The company’s fixed costs are $35,120 per annum.

,

• The company’s variable costs are $25 per component.

(a) The total number of component that the company needs to sell per annum to break-even is calculated thus:

`\begin{gathered} \text{ For break-even,} \\ Total\text{ }Revenue=Total\text{ }Cost \\ \therefore65x=25x+35120 \\ where\text{ }x=number\text{ }of\text{ }component \\ \Rightarrow65x=25x+35120 \\ 65x-25x=35120 \\ 40x=35120 \\ (40x)/(40)=(35120)/(40) \\ x=878 \end{gathered}`

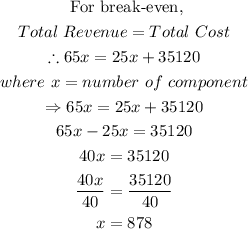
(b) The break-even in dollars is calculated as:

`\begin{gathered} Break\text{ }even(in\text{ }dollars)=65x \\ where\text{ }x=878 \\ Break\text{ }even=65(878) \\ Break\text{ }even=\text{ \$}57070 \end{gathered}`

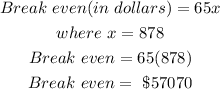
(c) The break-even as a percentage of the capacity is calculated thus:

`\begin{gathered} \%Break\text{ }even=(878)/(2722)*100 \\ \%Break\text{ }even=32.25569\% \\ \%Break\text{ }even\approx32\% \end{gathered}`

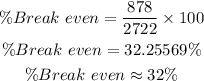
(d) If Alice produced and sold 1047 components in a year, we have:

`\begin{gathered} Total\text{ }revenue=65x=65(1047) \\ Total\text{ }revenue=\text{ \$}68055 \\ \\ Total\text{ }cost=25x+35120=25(1047)+35120 \\ Total\text{ }cost=\text{ \$}61295 \\ \\ \text{ Since the total revenue is greater than the total cost, she made a profit} \\ \therefore Profit=Total\text{ }revenue-Total\text{ }cost \\ Profit=\text{ \$}68055-\text{ \$}61295 \\ Profit=\text{ \$}6760 \\ \\ So,\text{ she made a profit of \$6760} \end{gathered}`

(e) In order to make a profit of $69,000 per year, the amount of components to sell is calculated thus:

`\begin{gathered} Profit=Total\text{ }revenue-Total\text{ }cost \\ 69000=65x-(25x+35120) \\ 69000=65x-25x-35120 \\ 69,000=40x-35120 \\ 40x=69000+35120 \\ 40x=104120 \\ (40x)/(40)=(104120)/(40) \\ x=2603 \end{gathered}`

Hence, the answers are:

`\begin{gathered} (a)\text{ }878\text{ }components \\ (b)\text{ \$}57070 \\ (c)\text{ }32\% \\ (d)\text{ \$}6760\text{ }profit \\ (e)\text{ }2603\text{ }components \end{gathered}`