Question

Pat was in a fishing competition atLake Pisces. He caught some bassand some trout. Each bassweighed 3 pounds, and each troutweighed 1 pound. Pat caught atotal of 30 pounds of fish.He got 5 points in thecompetition for each bass, butsince trout are endangered inLake Pisces, he lost 1 point foreach trout. Pat scored a total of42 points.how many bass and how many trout did pat Catch?I understand the method I'm supposed to use which is eliminationI'm struggling with how to actually set up the equation with the info from the word question

Answer 1

Answer: Pat caught 9 basses and 3 trouts

Let:

x = number of basses

y = number of trouts

Since Pat caught a total and 30 pounds, and each bass weighed 3 pounds while trouts weighed 1 pound, we can write this equation as:

`3x+1y=30\Rightarrow3x+y=30`

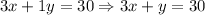
Then, it was stated that he got 5 points for each bass and lost 1 point for each trout. He then scored a total of 42 points. We can write this equation as:

`5x+(-1y)=42\Rightarrow5x-y=42`

We now have the equations:

3x + y = 30.........Equation 1

5x - y = 42..........Equation 2

We can solve this system of equations by elimination. Since we can see that we have a positive and a negative y, we can cancel this and solve for x.

Canceling y, we now have:

3x = 30

5x = 42

Add these two equations:

`3x+5x=30+42`
`8x=72\Rightarrow(8x)/(8)=(72)/(8)`
`x=9`

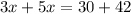
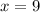
Then, we will substitute the value of x to any of the equations that we had to solve for y.

`3x+y=30`
`3(9)+y=30\Rightarrow27+y=30`
`y=30-27`
`y=3`

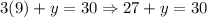
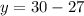
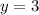
With these, we now know that Pat caught 9 basses and 3 trouts.