1 Answer

Edudepetris · Answer 1 · 2023-11-27T17:50:35+0000

The cosine rule in triangle ABC with sides a opposite to angle A, b opposite to angle B, and c opposite to angle C is

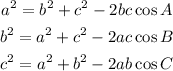
$\begin{gathered} a^2=b^2+c^2-2bc\cos A \\ b^2=a^2+c^2-2ac\cos B \\ c^2=a^2+b^2-2ab\cos C \end{gathered}$

From the given figure we can see triangle ABC with

$\begin{gathered} \angle C=39^(\circ) \\ a=26 \\ b=17 \end{gathered}$

Since angle C is the angle between sides a and b

Then we can use the cosine rule to find the length of the side c

The name of side c in triangle ABC is the side AB

Then we can use the cosine rule to find side AB

AB. Yes

Please log in or register to add a comment.