Given:
The equation of a line(preimage) is,
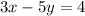
Rewriting the above equation, we get
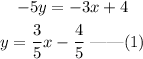
The general equation of a straight line is,

Here, m is the slope and c is the y intercept.
Comparing the above equations, we get that the slope of the line m=3/5 and the y intercept is -4/5.
The given line is dilated by a scale factor of 5/3 centered at the origin.
So, if (x,y) are the original coordinates of a point on the preimage of the line, then after dilation, the coordinates become (5x/3, 5y/3).
Replace (x,y) in equation (1) with (5x/3, 5y/3) to obtain the equation of the image of the line.
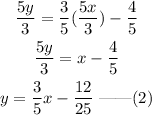
Comparing equations (1) and (2), we find that the slopes of the preimage and the image of the line has the same slope, but the y intercept changed.
Hence, the correct statement is "The image of the line has the same slope as the preimage but a different y-intercept."
Hence, option (a) is correct.