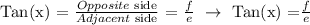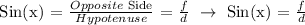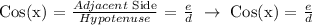From the figure, the following pieces of information are given:
x = angle
d = hypotenuse
f = opposite side
e = adjacent side
Let's recall the formula of the 3 main trigonometric functions and their ratios, then let's plug in the equivalent name of the lengths reflected in the figure:
We get,