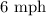Question

A boat can travel 30 miles against a current in the same time that it can travel 90 miles with the current. The rate of the current is 3 mph. Find the rate of the boat in Stillwater.

Answer 1

Let r represent the rate(speed) of the boat.

Given that the rate of the current is 3 mph, this implies that

`\begin{gathered} speed\text{ of the boat with current =\lparen r+3\rparen mph} \\ speed\text{ of the boat against current = \lparen r-3\rparen mph} \end{gathered}`

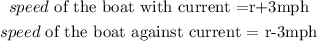
Recall that

`\begin{gathered} speed(rate)\text{ = }(d)/(t) \\ where \\ d\Rightarrow distance\text{ covered/traveled} \\ t\Rightarrow time\text{ taken} \end{gathered}`

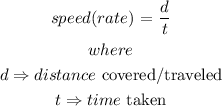
Thus, the time taken to travel 30 miles against the current is evaluated as

`\begin{gathered} r-3=(30)/(t) \\ cross-multiply, \\ t(r-3)=30 \\ \Rightarrow t=(30)/(r-3)\text{ ---- equation 1} \end{gathered}`

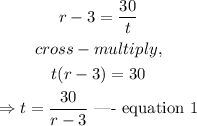
In a similar manner, the time taken to travel 90 miles with the current is evaluated as

`\begin{gathered} r+3=(90)/(t) \\ cross-multiply, \\ t(r+3)=90 \\ \Rightarrow t=(90)/(r+3)\text{ ----- equation 2} \end{gathered}`

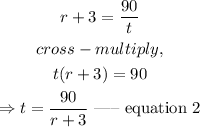
Given that the boat can cover these distances at the same time, this implies that we equate the time in equations 1 and 2.

Thus,

`(30)/(r-3)=(90)/(r+3)`

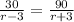
To solve for r, we cross-multiply

`30(r+3)=90(r-3)`

open parentheses,

`30r+90=90r-270`

collect like terms,

`\begin{gathered} 30r-90r=-270-90 \\ \Rightarrow-60r=-360 \end{gathered}`

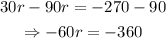
divide both sides by the coefficient of r.

the coefficient of r is -60.

thus,

`\begin{gathered} -(60r)/(-60)=-(360)/(-60) \\ \Rightarrow r=6\text{ mph} \end{gathered}`

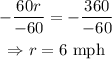
Hence, the rate of the boat in still water is

`6\text{ mph}`