We know that the focus is at the point F(-5,2); we also know that the directrix of the parabola is eight units to the right of the focus, which means that it passes through the point (3,2) and since it is a vertical line the equation of the directix is:

The equation of the axis of symmetry in this case must be horizontal and it is given as:
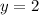
To find p we first need to find the distance between the two points we discussed earlier, then we will divide by two since the distance between the directix and the focus is twice the value of p. The distance between two poitns is given by:
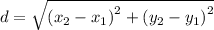
Plugging the values of the points we have:

Hence the absolute value of p is:
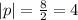
Now, since the directix is to the right of the focus this means that the parabola has to open to the left which implies that p has to be negative. Hence:
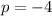
Once we know p we can find the vertex of the parabola. Since the parabola is horizontal and we know it opens to the right we just need to add the absolute value of p to the x-coordinate of the focus, hence we have:
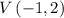
Finally we can find the equation of the parabola:
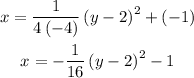
Therefore, the equation of the parabola is:

The graph of the parabola, axis of symmetry and directrix are shown below: