(3 ^(3) - 2x ^(2) + 3x - 4) / (x - 3)perform to find the value of the remainder

Question

`(3 ^(3) - 2x ^(2) + 3x - 4) / (x - 3)`perform to find the value of the remainder

Answer 1

The remainder of the division is 68 (OPTION A)

SOLUTION

Problem Statement

We are given the following polynomial division:

`(3x^3-2x^2+3x-4)/(x-3)`

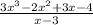
We are asked to find the remainder of the division.

Method

To find the remainder, we should apply the Remainder theorem of polynomials. The Remainder theorem of polynomials states that:

"It states that the remainder of the division of a polynomial F(x) by a linear polynomial x - r is equal to F(r)", where r is a real number.

Implementation

Before applying the theorem stated above, we need to identify F(x) and the linear polynomial (x - r) from the question.

`\begin{gathered} \text{The polynomial }f(x)\text{ is:} \\ 3x^3-2x^2+3x-4 \\ \\ The\text{ linear polynomial (x-r) is:} \\ (x-3) \\ \text{ In this case, r = 3} \end{gathered}`

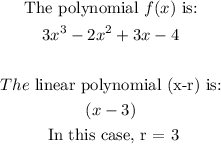
Thus, to find the remainder, we just need to find F(3), which is simply substituting 3 in place of x into the polynomial f(x).

This is done below:

`\begin{gathered} f(x)=3x^3-2x^2+3x-4 \\ \text{put x = 3} \\ f(3)=3(3^3)-2(3^2)+3(3)-4 \\ f(3)=81-18+9-4 \\ \\ \therefore f(3)=68 \end{gathered}`

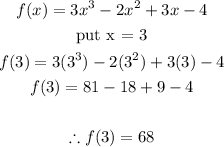
Final Answer

Thus, the remainder of the division is 68