The given equation is:
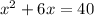
Firstly, we are going to transfer +40 to the left hand side of the equation and this becomes:
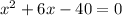
Secondly, we can use the method of factorization to solve the equation above, by finding the factors of 40, such that when multiplied gives -40 and when added gives +6.
The required factors for this are +10 and -4.
Thus, we have:
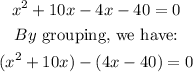
This becomes:
![undefined]()