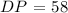Question:
Solution:
Consider the following diagram that represents the given problem:
Now, since P is the midpoint of DE, we get the following equation:
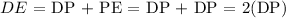
According to the diagram, this is equivalent to:
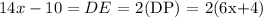
this is equivalent to:
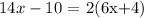
Applying the distributive property, this is equivalent to:
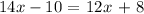
putting together similar terms, this is equivalent to:
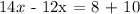
this is equivalent to:
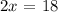
solving for x, we get:
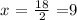
replacing this into the following equation:
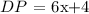
we get:
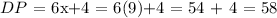
so that, we can conclude that the correct answer is: